我女朋友约会总爱迟到，比如本来约好的19:00餐厅见面，总能给我19:30才到，于是我想了一个办法，告诉她说我们18:30见面，然后她不就正好19:00到，符合我的心理预期了吗（虽然事实证明我还是太天真，不过这是后话）？我今天想跟大家分享的是，当我们在进行临床样本量计算的疗效预估（Effect Size Assumption）和最终试验成功（Reject H₀）的界值（Boundary）之间的关系与区别，大家可以对应一下，疗效预估和界值，哪一个是18:30，哪一个是19:00。

1. 从单臂试验说起

假设有一个罕见肿瘤的确证临床单臂设计需要你进行样本量计算，假设经过与MM“友好”的沟通，已经告知了你以下参数：

药物的预估疗效： Confirmed ORR = 30%
临床有意义对照：ORR = 10%
α=0.025
β=0.1

考虑到在进行率的单臂样本量考量时n和Power的锯齿状关系（如下图所示），我们会选择一个Power不会再下降到90%以下的n，如45。

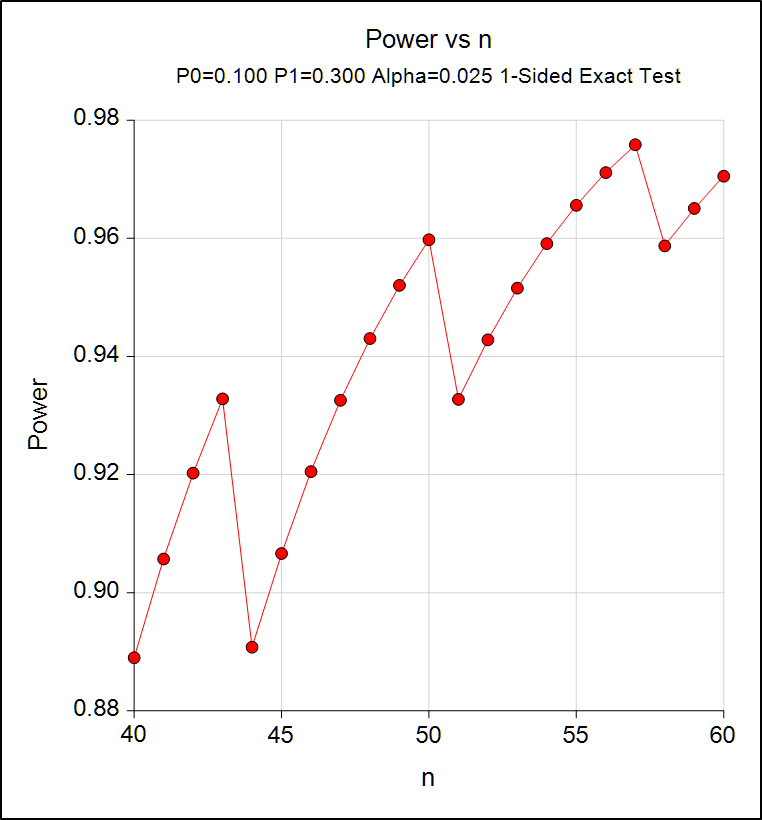
图1.1 样本量和把握度的关系

一般来说，商用的样本量计算软件都会在最后得出一个结论，类似“Reject H₀ If R ≥10”，也就是意味着当45例受试者中有10例达到response，你这么一算，发现10/45 = 22.2%，直觉告诉你，something is wrong，但是实际上，这个22.2%（boundary）与30%（effect size assumption）有联系并不相同，一个是统计学拒绝H₀的成功最低标准，另一个是在样本量计算阶段的预设，预设是有冗余的，就像我跟女朋友约定见面时间一样，而拒绝H₀的标准是严格的，就像我最晚可以接受的见面时间一样，再晚我可能会骂她一顿（事后还得哄- -!）。好了，到了现在，我们应该了解到疗效预估和界值的区别，那么除了单臂设计之外，常规的1∶1临床试验如何在试验未开展前得出boundary，做到心中有数呢？

2. Boundary的计算

2.1 基础公式

说起来界值，总有种似曾相识的感觉，非劣效界值吗？好像没啥关系。我是在哪里提到过来着？没错，就是成组序贯设计的试验中，在期中分析时，存在有效终止和无效终止界值，有具体的计算方式可以得出界值，那么我们可以不可以直接利用相关的公式，计算fix-design下的界值呢？

经过深究了gsDesign包的源代码，对于正态分布终点，得出了如下用来计算其boundary的公式：

\hat{\Delta} = \frac{\left| Z_{\alpha/2} \right|}{\sqrt{n}} \cdot \frac{\Delta_1 - \Delta_0}{\Delta + \Delta_0}\tag{1}

其中参数的代表如下表格所示：

参数	含义
\hat{\Delta}	界值
Z_{\alpha/2}	标准正态分布的Z值
{n}	样本量
\Delta_1	备择假设下试验组和对照组的疗效差值
\Delta_0	零假设下试验组和对照组的疗效差值
\Delta	标准化后的疗效差值 \Delta = \frac{\Delta_1 - \Delta_0}{SE} SE = \sqrt{ \frac{SD_1^2}{\frac{ratio}{1 + ratio}} + \frac{SD_2^2}{\frac{1}{1 + ratio}} }

我们现在假定有一个1∶1的临床试验，有以下的参数设置用来计算样本量：

参数	含义
\alpha	0.05
\beta	0.1
Ratio	1
\Delta_1	-10
\Delta_0	0
SD	20
n	n = \left( \frac{Z_{\alpha/2} + Z_{\beta}}{\Delta} \right)^2=168.10\approx 170
\hat{\Delta}	?

根据我的前面提到的式(1)，可以得出\hat{\Delta}=-6.01，也就是说基于 \Delta_1 = -10的疗效假设，其界值应至少小于-6.01，才有较大可能拒绝H₀。

2.2 便于计算

有同学提到，难道我每次计算boundary时，都要套公式吗？当然，我们也可以直接借用gsDesign包的shiny来进行计算（我太懒了！忏悔，等有时间一定把其他终点直接计算的公式补充上）。依旧是选用上面的正态数据分布的参数，如下所示：

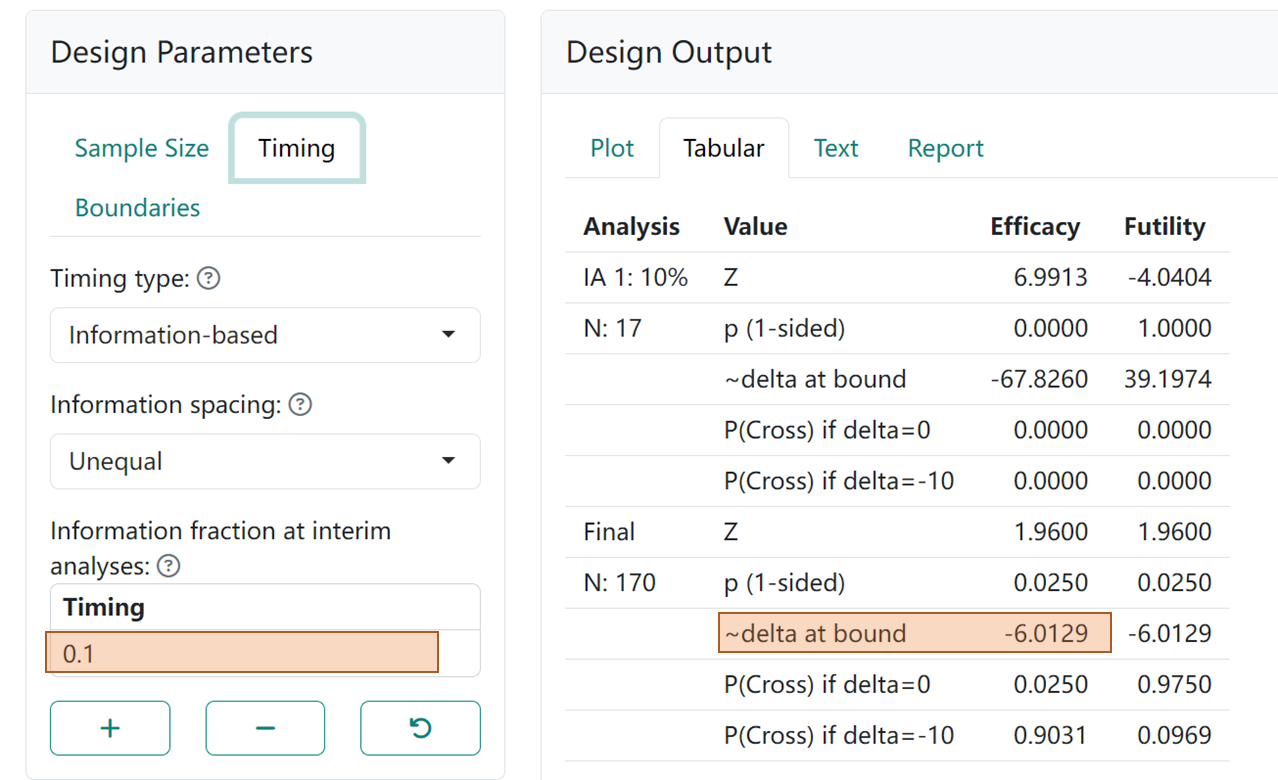
图2.1 gsDesign shiny app 示意图

键入一个较小的Timing值，可以得到对应的Boundary，也就是-6.01，跟公式算出的几乎没有差异。其他类型终点也可以用相同的方法计算得出。

3. 关于Boundary的准确性-模拟验证

也许有的同学会质疑该方法算出的boundary是否代表真实值，还记得我前面提到的“才有较大可能拒绝H₀。”有请注意我说的是有较大可能，为什么这么说呢？因为自从统计学引入了数学之后，其就成为了从不完美中追求最合理的解释的科学。即使最终结果显示-6.01,也并不一定会拒绝零假设，因为这些推断是需要一些前提条件的，在这个例子中其需要满足正态分布，而且标准差不能超出预期，-6.01才变得更接近真实值，更何况在实际的临床试验中还存在一些协变量需要调整的问题。下面我们看来一个简单的模拟：

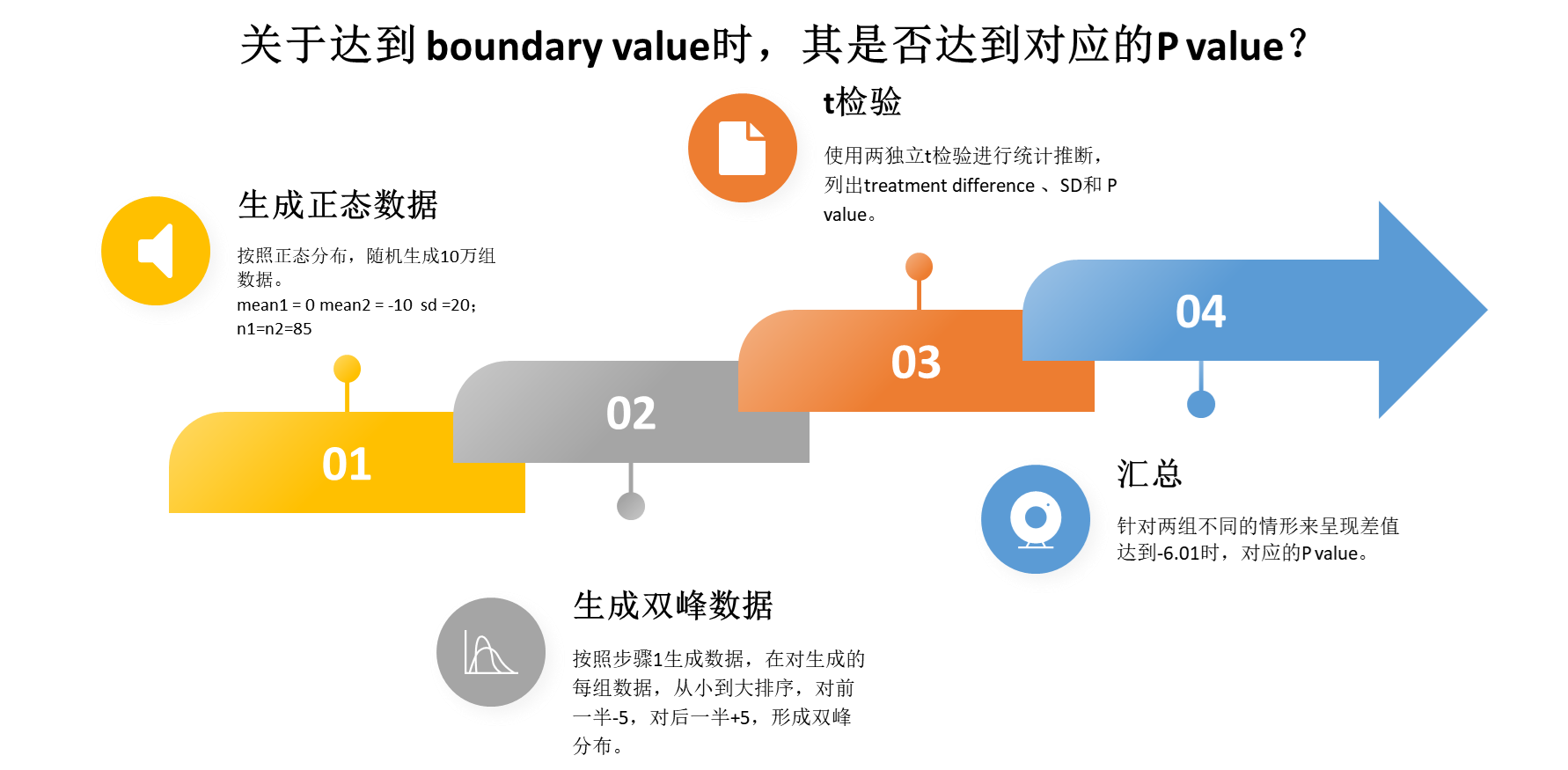图2.2 模拟步骤

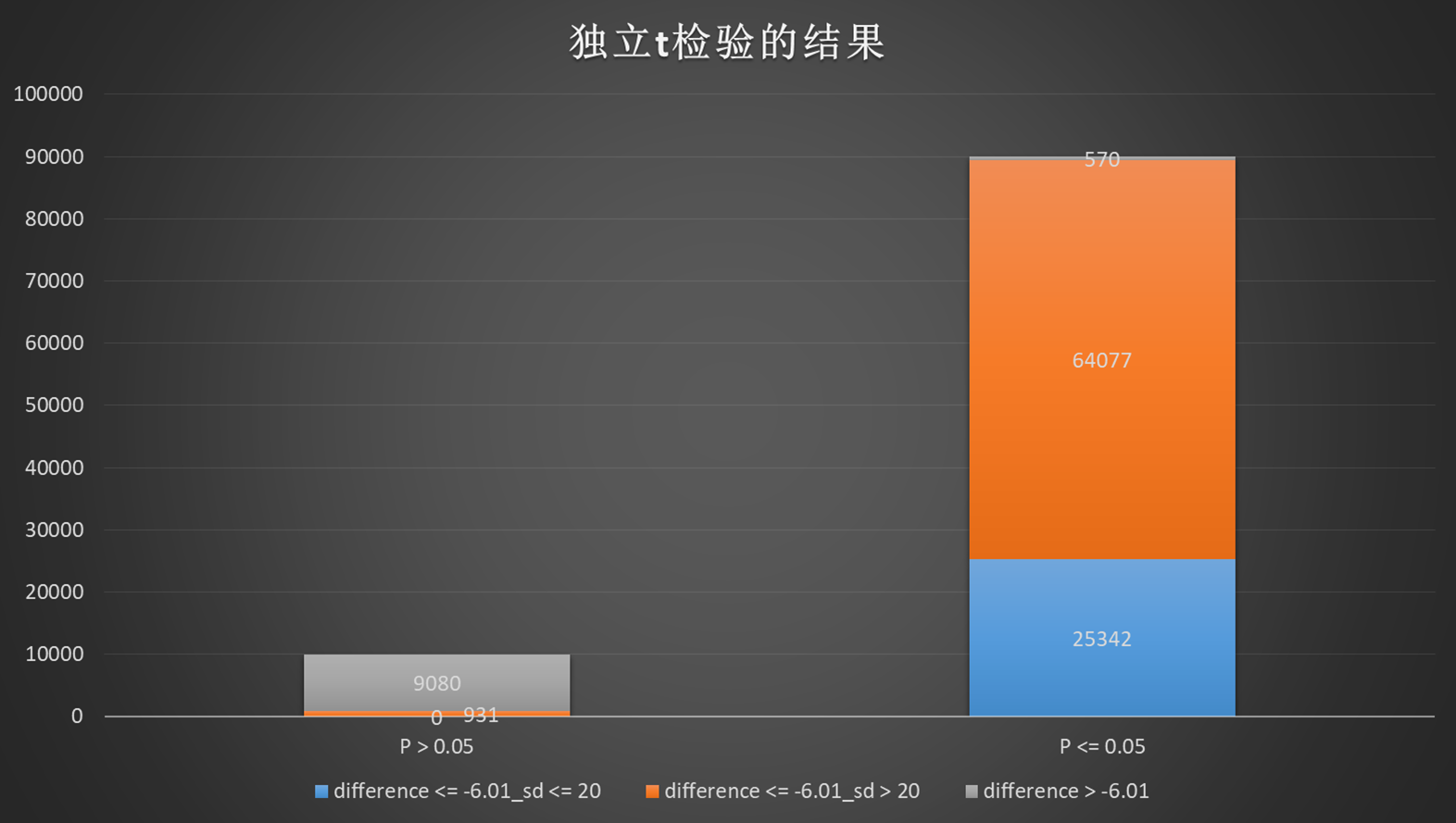
图2.3 正态数据的检验结果

可以看出，在正态分布下，当difference 小于-6.01时且SD不超出预期太多时，可以拒绝H₀得出试验组和对照组有统计学差异的结论，蓝色图例和橙色图例。

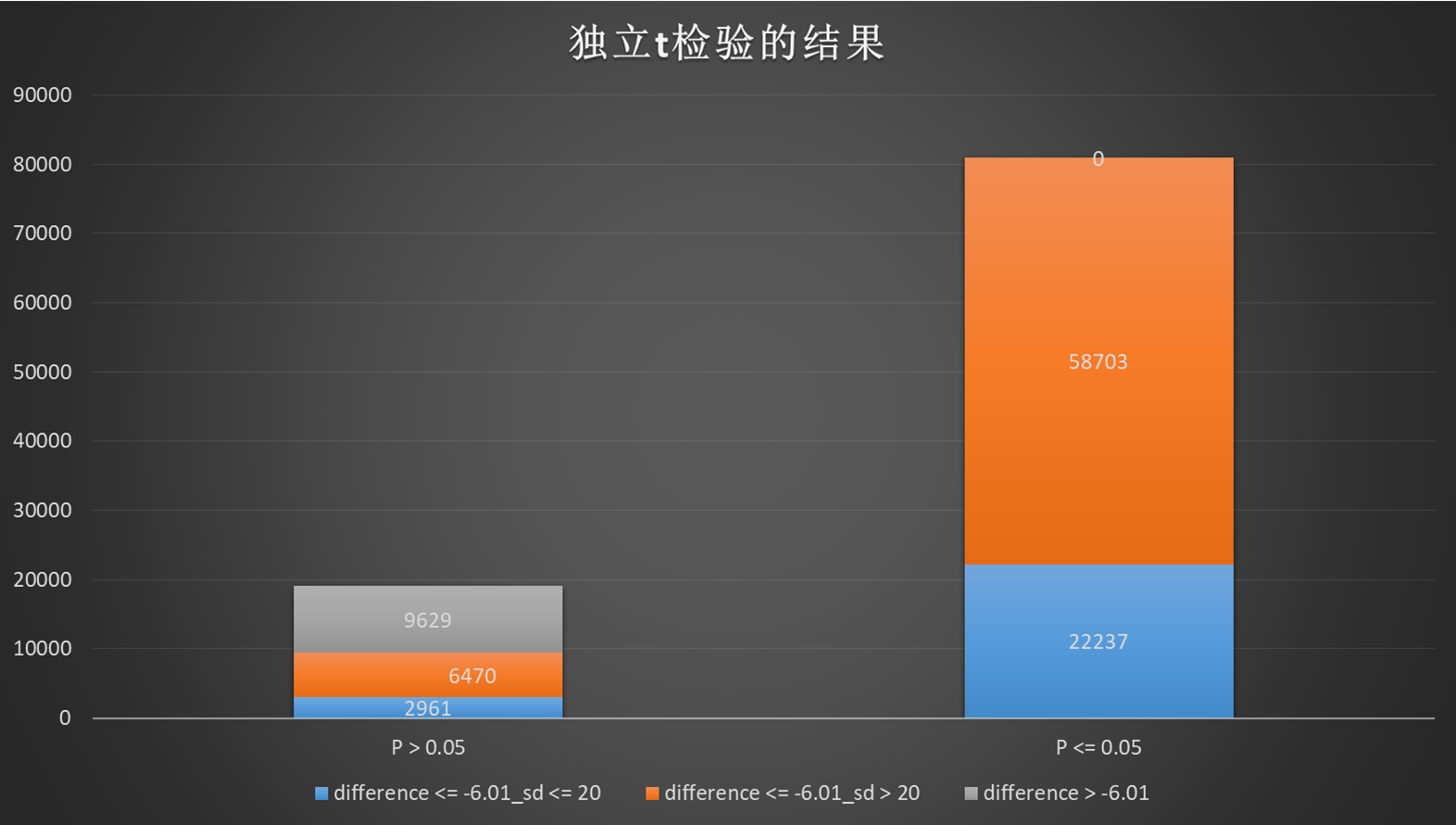
图2.4 双峰数据的检验结果

可以看出，在非正态分布下，当difference 小于-6.01，SD ≤20时，不一定会得出拒绝H₀的结论，也就是蓝色图例。