写在前面：本系列文章主要参考了北卡罗来纳州立大学的ST 520讲义中的 Early Stopping of Clinical Trials 章节（https://www4.stat.ncsu.edu/~dzhang2/st520/520notes.pdf），并基于潘老师的三期临床设计-成组序贯的视频（https://www.bilibili.com/video/BV1jy4y1k7eW/?spm_id_from=333.999.0.0）进行了部分的补充和说明。

前言

在临床试验进行过程中，有很多的原因会导致其提前终止，如药物的严重毒性或不良事件、疗效已得到证实（有或无）、申办方本身的原因、难以弥补的设计或其他的重大缺陷等。由于临床试验前期（无论是科学上、情感上、财务上等方面）已经投入了绝大部分资源，因此设计或参与临床试验的研究人员可能不是决定是否应该终止临床试验的最佳人选。对于大样本的Ⅲ期临床试验来说，成立数据安全监察委员会（Data Safety Monitoring Board，DSMB）依照方案对进行中的临床试验中不断累积的安全性和有效性数据进行审阅，并向申办方给出试验是否应当终止的建议成了常见的选择（当然，过于DSMB的职责及什么时候应该设立，以及具体实施过程中的细节，以后可以单独展开讲）。

那么DSMB依据什么准则进行试验终止的判断呢？选择之一就是采用成组序贯设计（Group-sequential Design），成组序贯设计就是在期中分析节点时，通过衡量组间的治疗效应来对是否提前终止试验进行判断的方法。

适用条件

• 该研究的数据是随着时间的推移而收集的，无论是新入组的受试者还是已经入组的受试者。

• 感兴趣的是使用数据来回答医学问题。一般经常将其建立在假设检验框架下。

• 独立的数据监察委员会每隔一段时间就会来评估现阶段是否有“足够强的证据”来拒绝原假设并有望提前终止试验。

• 在每次评估时，都会使用统计量来与界值进行比较。每次评估的界值在方案中需要提前规定，如果超过了界值，那么可以认为有足够的证据来终止试验。一般来说，被计算的统计量应较好的服从正态分布。

• 界值的选择基于一开始的样本量设计中的显著性水平（level）和把握度（power）。

基于信息的设计和监察（Information based design and monitoring）

H_{0} :\Delta =0

H_{1} :\Delta \ne 0

其中，Δ代表了感兴趣的终点参数，然后我们用θ代表干扰参数（nuisance parameters）。以上为双侧检验，如果为单侧检验时，写成如下形式：

H_{0} :\Delta \le 0

H_{1} :\Delta > 0

注意：以上提到的假设检验都是本系列文章的基本框架。

在任意的期中分析的时间点t，我们的关于试验是否提前终止的决议将会基于统计量：

T(t)=\frac{\hat{\Delta } (t)}{se\left \{ \hat{\Delta } (t) \right \} }

其中\hat{\Delta } (t)是\Delta的估计值，se\left \{ \hat{\Delta } (t) \right \} 代表的是\hat{\Delta } (t)的标准误，其使用的是到达时间t的所有的累计的数据；对于双侧检验来说，当\left | T(t)\right | 足够大时则可以拒绝零假设，接受备择假设，单侧检验同理。

以上提到的为连续变量的情形，对于二分类和时间-事件终点，表格如下展示：

讨论到更一般的情形时，假定一个参数模型其服从p(z;Δ,θ)，在时刻t，我们使用极大似然估计的\hat{Δ} (t)来代表Δ，使用逆观测信息矩阵的平方根（ the square-root of the inverse of the observed information matrix）计算得出的se\left \{ \hat{\Delta } (t) \right \} 来估计标准误。

如果Δ=Δ^{*}，即满足备择假设，则检验统计量服从如下的正态分布：

T(t)=\frac{\hat{\Delta } (t)}{se\left \{ \hat{\Delta } (t) \right \} } \stackrel{Δ=Δ^{*}}{\sim}N(\Delta^* I^{1/2}(t, \Delta^*), 1),

这里的I(t, \Delta^*)代表了t时刻的统计信息，这里的统计信息指的是费舍尔信息量，如果你不是特别熟悉这些概念，为了实际应用的考虑，我们可以将其等于（至少近似于）估计的标准误，也就是说：

I(t, \Delta^*) \approx \left \{se(\hat{\Delta}(t))\right \} ^{-2}

如果Δ=0，即满足零假设，则检验统计量服从标准正态分布：

T(t)\stackrel{Δ=0}{\sim}N(0,1),

上式为成组序贯检验的基础之一。加入，我们想进行一次双侧检验，我们则在如下条件下拒绝零假设：

\left | T(t) \right | \ge b(t),

这里的b(t)是临界值，或者我们常称之为界值。如果我们仅分析一次，并且在检验水准为α时进行统计学检验，那么我们会选择b(t)=Z_{\alpha/2}。因为在零假设下的T(t)服从N(0,1)，那么则有：

P_{H_0}\{|T(t)| \geq Z_{\alpha/2}\} = \alpha.

然而，成组序贯需要考虑K个不同时间点的数据，假设t₁,…，t_K，如果在任意时间点检验统计量足够大，我们有K次机会拒绝零假设，如果我们恰当的选择每次分析的界值，则有：

|T(t_j)| \geq b(t_j),

备注：如果用概率表示，拒绝零假设则对应着如下事件，只要有一个事件大于界值就拒绝零假设：

\bigcup_{j=1}^{K} \left\{|T(t_j)| \geq b(t_j)\right\}.

同样的，接受零假设对应着如下事件，所有的事件都小于界值则接受零假设：

\bigcap_{j=1}^{K} \left\{|T(t_j)| < b(t_j)\right\}.

关键的问题就在于，在期中分析时治疗效应多大才能够拒绝零假设；也就是说我们如何选择界值？更进一步的说，这种成组序贯检验的策略对检验水准和把握度有什么后果，并且是如何影响样本量计算呢？

Ⅰ类错误（Type Ⅰ error）

在进行成组序贯设计多个时间点的检验量显著性的比较时，如果我们简单将首次出现检验统计量大于1.96就拒绝H₀，那么多重比较会导致Ⅰ类错误的膨胀，也就是：

\text{type I error} = P_{H_0}\left(\bigcup_{j=1}^{K} \left\{|T(t_j)| \geq 1.96\right\}\right) > .05,

如果K\geq2

在如下的表格中列出了Ⅰ类错误膨胀的具体数值：

表10.1: 多次分析对于Ⅰ类错误影响

像是Jerome Cornfield (1912–1979)说过的那句话：

Sampling to a foregone conclusion

在这一章，我们的首要目的就是在控制Ⅰ类错误条件下得出成组序贯中的界值。

检验水准α

当零假设为真时，我们要将拒绝H₀的概率控制在0.05。以下是检验策略全部可能的情形：

• 在第一次期中分析时拒绝H₀并停止试验，如果：

\left\{|T(t_1)| \geq b(t_1)\right\}

• 或在第二次期中分析时拒绝H₀并停止试验，如果：

\left\{|T(t_1)| < b(t_1), |T(t_2)| \geq b(t_2)\right\}

• 或…

• 或在最后一次期中分析时拒绝H₀并停止试验，如果：

\left\{|T(t_1)| < b(t_1), \ldots, |T(t_{k-1})| < b(t_{k-1}), |T(t_k)| \geq b(t_k)\right\}

• 或者是接受H₀，如果：

\left\{|T(t_1)| < b(t_1), \ldots, |T(t_k)| < b(t_k)\right\}.

这些表达式把样本空间分为了多个拒绝域和一个接受域。为了我们的检验过程基于水准α，那么这些界值b(t₁),…,b(t_K)必须满足：

注意：

为了满足(1)，等式左边的部分包括了多元统计量(T(t₁),…,T(t_K)的联合分布。因此，为了在规定的检验水准下得出必要概率，在零假设下，我们需要知道在t₁,…t_k时刻的顺序检验统计量的联合分布。类似的，在备择假设下，同样需要知道该检验统计量联合分布。

我们主要依靠以下的方法学来监测临床试验得到我们的主要结果：

任何基于疗效的检验或估计量，针对∆，进行恰当标准化后，当随时间连续计算时，渐近地，具有一个正态独立增量过程，其分布仅依赖于参数∆和统计信息。

Any efficient based test or estimator for ∆, properly normalized, when computed sequentially over time, has, asymptotically, a normal independent increments process whose distribution depends only on the parameter ∆ and the statistical information.

Scharfstein, Tsiatis and Robins (1997). JASA. 1342-1350.

在上一章，我们已经提到过当Δ=Δ^{*}，即满足备择假设，则检验统计量服从以下的正态分布：

T(t)=\frac{\hat{\Delta } (t)}{se\left \{ \hat{\Delta } (t) \right \} } \stackrel{Δ=Δ^{*}}{\sim}N(\Delta^* I^{1/2}(t, \Delta^*), 1),

我们对该检验统计量进行如下的正态化，令：

W(t) = I^{1/2}(t, \Delta^*)T(t),

当我们在计算每个时间点t₁<t₂<…<t_k的统计量时，那么多元向量的联合分布为}W(t₁),…,W(t_K)}近似正态分布，并且有均值向量{∆^∗ I(t₁, ∆^∗ ), . . ., ∆^∗ I(t_K, ∆^∗ )}和协方差矩阵：

\text{cov}[W(t_j), \{W(t_\ell) - W(t_j)\}] = 0, \quad j < \ell, j = 1, \ldots, K.

上式之所以等于0就应用了独立增量的结论，即下一个时间点相对于上一个时间点的增加的信息相对于上一个时间点是独立的，故其协方差矩阵等于0。

我们也可以将每个时间点的W(t_j)写作：

那么对于j < \ell：

实际上我们感兴趣的变量为T(t_j)，那么将上式反写回来，有：

那么这也意味着{T(t₁),…,T(t_K)}的联合分布也是多元正态分布，其中的均值则为：

协方差矩阵则为：

那么对于j < \ell，协方差则为：

总的来说，T(t_j)和T(t_ℓ)协方差为在时间t_j和t_ℓ的信息量比值的平方根。因为，在零假设下，即Δ=0时，顺序计算的检验统计量(T(t₁),…,T(t_K))也是多元正态分布，其均值为0，其协方差矩阵如下（在该情形下为相关矩阵，因为方差均为1）：

这个结果的重要性就在于，在零假设下，按顺序计算的检验统计量的联合分布完全由各个时间点的信息的比值来决定。这也就允许我们评估在（1）式中的的概率，用来找到恰当合适的界值b(t₁​),…,b(t_k​)来进行Ⅰ类错误的控制。

相等的信息增量

让我们考虑一种特殊的情形，即每次的信息增加都是相等，即：

注意：如果我们感兴趣的疗效的响应是瞬时（instantaneous）的问题，那么无论这种响应是离散的还是连续的，信息量与当下研究的受试者数是成比例的。在这个情形下，在相等的信息增量后计算检验统计量与在相等的受试者进入研究进行统计计算是等价的。所以，假设入组100例受试者来比较一个临床试验组间响应率的差别，那么我们也许会在相等的信息增量后进行五次的监测；也就是每20个人进行一次。

如果在信息量等增长的情形下，监测一项研究K次，在零假设下，用于构建群体序贯检验的序贯计算检验统计量将具有一个非常特定的分布结构。因为I(t_j​,0)=jI，j=1,…,K，这意味着序贯计算检验统计量{T(t₁​),…,T(t_K​)}的联合分布是一个多变量的正态分布，其均值向量等于0，并且根据(5)式，其协方差矩阵等于：

这意味着在零假设下，一旦我们知道预期分析的总数K，那么在信息量等长后计算出的序贯检验统计量的联合分布就完全确定了。现在，我们可以计算这样的概率：

那么为了满足检验水准为α的成组序贯设计，为了能够得到界值b₁,…,b_k使得上述的概率等于1-α是所必须的。

注意：为了计算具有协方差结构（6）的多元正态分布的积分，可以通过使用阿米蒂奇（Armitage）、麦克弗森（McPherson）和罗（Rowe）在1969年首次提出的递归数值积分法来快速完成。这种方法利用了联合分布是独立正态随机变量的标准化部分和的事实。这种积分法允许我们搜索满足条件的不同组合 b1, ..., bK，从而满足：

实际上存在无限组合的边界值，可以将Ⅰ类错误控制在α水平；因此，我们需要评估这些不同组合的统计后果，以帮助我们在选择使用哪些组合时做出决策。

界值的选择

刚才提到了如果没有其他的限制条件，那么界值有无穷多的组合。Wang 和 Tsiatis（1987）在Biometrics提出了一种灵活界值的限定方法。我们现在会首先讨论等信息增量的情形，稍候会对其进行推广。这个函数是由功率函数来特征化，我们将其表示为Φ，具体来说如下表示：

不同的Φ值决定了随时间变化不同的界值的形状。我们也会把Φ叫做形状参数。

当Φ取任意值时，我们都可以在显著水平α下得出常数c：

回顾：在零假设下，且信息量是等量递增的情形，则{T(t₁), . . ., T(t_K)}的联合密度完全已知。我们将得到的解表示为c(α，K，Φ)，一些可能的情形如下（表中列出的为c值）：

表10.2: 对于选定的α，K，Φ，双侧检验的成组序贯界值

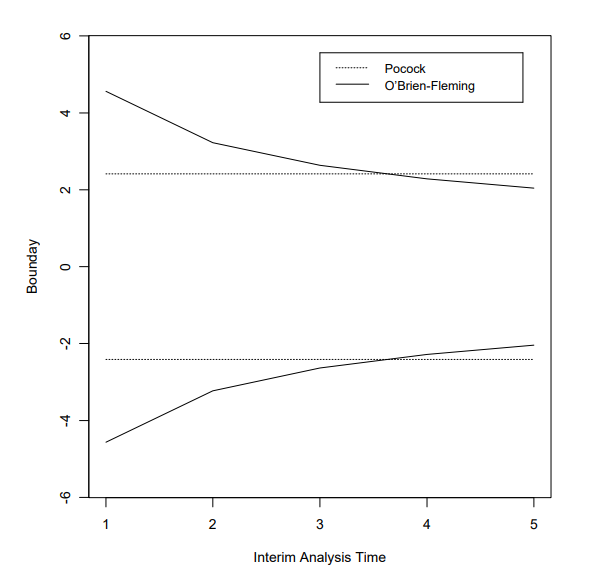
举例：在上面提到的例子中，有两种特殊的界值选择方法已经在文献中和实践中进行了广泛的讨论。就是当Φ=0.5和0.0的时候。当 Φ = 0.5 时的第一个边界是 Pocock 边界（Pocock 1977年 Biometrika），而当 Φ = 0 时的另一个边界是 O’Brien-Fleming 边界（O’Brien 和 Fleming 1979年 Biometrics）。

Pocock boundaries

当成组序贯检验使用Pocock界值在首次拒绝原假设的期中分析(t_j，j=1,…,K)如下所示:

也就是说，当使用累计的数据进行标准化的统计学检验时，如果其超过某个常数就会拒绝原假设。

举个例子，如果我们取K=5和α=0.05，那么根据表10.2，c(0.05,5,0.5)=2.41。因此，将显著性水准控制在0.05，计算得出的统计量在信息等量递增的情形下会被计算至多5次，直到有一次超过界值2.41；也就是说，只要|T(tj)| ≥ 2.41，我们拒绝零假设。这也等价于其任意一次P值小于0.0158。对应的R codes如下：

library(gsDesign)
po_bound <- gsDesign(k = 5, sfu = "Pocock", test.type = 2, alpha =0.025)$upper$bound
po_bound
(1-pnorm(po_bound,0,1))*2

O’Brien-Fleming boundaries

O’Brien-Fleming界值的形参为Φ=0。使用O’Brien-Fleming界值的成组序贯检验设计首次拒绝原假设的期中分析(t_j，j=1,…,K)如下所示:

举例，如果我们依旧选择K=5和α=0.05，那么根据表10.2，c(0.05,5,0.0)=4.56。因此，使用O’Brien-Fleming界值我们将会在如下情形时首次拒绝原假设：

因此，在这个例子中，五个界值依次为b₁ = 4.56, b₂ = 3.22, b₃ = 2.63, b₄ = 2.28, b₅ = 2.04，R代码如下：

of_bound <- gsDesign(k = 5, sfu = "OF", test.type = 2, alpha =0.025)$upper$bound
of_bound
of_bound[1]/sqrt(1:5)
(1-pnorm(of_bound,0,1))*2

表10.3 K=5 α=0.05的正态化P值

以上提到的两种界值的形状如下图所示：

图10.1 Pocock and O’Brien-Fleming Boundaries

Lan-DeMets Spending Function

Lan和DeMets在1983年首次提出使用消耗函数来为群组序贯试验设定边界的方法。在这篇文章中，他们提出了两个具体的消耗函数：一个用于近似O'Brien-Fleming设计，另一个用于近似Pocock设计。也是现阶段在临床试验中最为常用的界值判定方法。

在param=1=rho，有近似OBF的消耗函数：

当param在区间 [0.005,2]之外，rho=1时，有近似Pocock的消耗函数：

对应的R codes为：

ld_of_bound <- gsDesign(k = 5, sfu = sfLDOF, test.type = 2, alpha =0.025)$upper$bound
ld_of_bound 
of_bound <- gsDesign(k = 5, sfu = "OF", test.type = 2, alpha =0.025)$upper$bound
of_bound

ld_po_bound <- gsDesign(k = 5, sfu = sfLDPocock, test.type = 2, alpha =0.025)$upper$bound
ld_po_bound
po_bound <- gsDesign(k = 5, sfu = "Pocock", test.type = 2, alpha =0.025)$upper$bound
po_bound

从信息的角度来看效能和样本量

在上一章节我们已经讨论了如何在提前定义的检验水准α下构建成组序贯检验统计量。但与此同时我们也需要考虑成组序贯检验统计量对把握度和样本量可能造成的影响。为了方便理解，我们首先会复习一下在只进行一次分析时如何考虑把握度和样本量。

像是前面提到的，在时间点t计算得出的检验统计量的分布：T(t)，在零假设下有：

对于有临床意义的备择假设，即Δ=Δ_A则有：

这里代表统计信息量的I(t, \Delta_{A})可以通过[\mathrm{se}\{\hat{\Delta}(t)\}]^{-2}来近似，这里的\Delta_{A}I^{1/2}(t, \Delta_{A})代表非中心化参数。为了在检验水准双侧α=0.05的情形下，有足够的把握度1-β来得出备择假设Δ_A有临床意义，有如下推导：

从上式中可以看出检验的把握度直接与统计量信息相关。因为信息近似的等于[\mathrm{se}\{\hat{\Delta}(t)\}]^{-2}，这也就意味着该研究要持续的收集足够的数据直到确保：

因为有一种策略就是为了确保足够的把握度来得出临床的重要差异，需要持续不断的监测标准误直到估计的差值在时间t进行唯一一次最终的分析：

使用如下的检验来拒绝零假设，当：

注意：我们在使用基于信息的方法时，并没有规定任何多余的参数。该方法的达到把握度的准确取决于该分布有多近似于正态分布并[\mathrm{se}\{\hat{\Delta}(t^F)\}]^{-2} 有多近似于Fisher信息量。基于初步的一些数据模拟显示，如果在Ⅲ期临床试验中样本量足够大，那么该基于信息的方法表现很好。

实际情况是，我们不可能告诉研究者在一个临床试验中持续的收集数据直到治疗差异的标准误足够小（信息量足够大），而不告知这个试验需要多少资源（像是样本量、试验的持续时间等）。一般来说，在试验设计阶段，我们会对多余参数进行一些猜想并且据此来进行最初的的试验设计。

举个例子，如果我们为了比较两个治疗组，1和0的反应率的差别，即π₁-π₀，而π_j代表就是总体中治疗组1和0的反应率的差值。那么，在时间t时，我们通过样本中疗效的差距\hat{\Delta}(t) = p_1(t) - p_0(t),其标准误为：

因此，为了保证有足够的把握度拒绝零假设，则在总体疗效假设为\Delta(t) = π_1(t) - π_0(t),时，我们将会需要如下的样本量：

注意：上面的样本量公式是通过如下的检验统计量来比较治疗的反应率差距：

严格说起来，尽管在两组相等随机和大样本的情况下，上式与比例检验（下式）差别微乎其微，但两者并不相同：

这里比较重要的一点就是，把握度受我们从现有数据中关于感兴趣参数的统计信息量的驱动。数据越多，我们拥有的信息就越多。要达到 1 - β 的把握度，以检测在 α 显著性水平上使用双侧检验的临床重要差异 ∆_A，意味着我们需要收集足够的数据，以使得统计信息量等于：

让我们探讨把握度和信息如何与成组序贯检验相关。如果我们计划在信息等量增加情形下进行 K 次中期分析，那么分组顺序检验检测替代假设 ∆ = ∆_A 的把握度由以下给出：

为了计算出上式给出的事件的概率，我们需要知道在备择假设下向量\{T(t_1), \ldots, T(t_k)\}的联合分布。

我们用MI来代表最终分析时的最大信息量。那么一个具有信息等量增加和最大信息 MI 的 K-次成组序贯设计，则会在 t_j 时刻进行中期分析，如下所示：

使用(2)-(4)、(8)式的结果，可以得到\{T(t_1), \ldots, T(t_k)\}r

并且可以根据(6)式得到它的协方差矩阵V_T。如果我们定义：

那么均值向量则等于：

使用Wang-Tsiatis界值的成组序贯设计在显著性水准α上某次拒绝原假设时：

对于备择假设H_A：Δ=Δ_A最大信息量MI，那么该检验的把握度为：

这里的\delta = \Delta_A \sqrt{MI},，并且\{T(t_1), \ldots, T(t_k)\}服从多元正态分布，其均值向量为(9)式，协方差矩阵服从(6)式。当α、K、Φ取固定值时，把握度是关于δ的递增函数，这里的δ可以使用递归积分求解。那么，我们可以在把握度达到1-β时的δ值。我们使用δ(α, K, Φ, β) 来表示这个解。

注意：δ的值与非中心参数有着类似的作用。因为\delta = \Delta_A \sqrt{MI},这意味着一个以α为检验水准，Φ为形状参数的成组序贯设计，随着需要计算的信息等量的增加，直到K次得出的最大信息量等于：

或：

则有足够的把握度1-β检测出临床差异Δ=Δ_A。

膨胀因子

那么在得到了最大信息量后，它是如何影响样本量的呢？一个有用的方法就是将其与提前定义好power下的固定样本量设计进行关联。在公式(7)中，我们认为，使用固定样本检验在α水平下检测替代假设∆ = ∆_A并具有1 − β的效能所需的信息量是：

相比之下，在相同的检验水准和效能下，使用形状参数Φ的K次成组序贯检验来检测相同替代假设所需的最大信息量是：

这里的

叫做膨胀因子，或者是成组序贯设计相对于固定样本设计在保持相同把握度的情况下所需的信息量增加。

备注：膨胀因子不取决于感兴趣的终点或被认为临床上重要的治疗差异的大小。它仅取决于检验水准（α）、把握度（1 − β）和成组序贯设计的参数（K, Φ）。对于一些成组序贯检验的膨胀因子已经制成表格，如下所示：

表10.4 不同类型的界值及K，α，β取值下的膨胀因子

上表方便了使用成组序贯设计研究的样本量计算，因为它可以建立在传统用于固定设计的样本量计算方法之上。例如，如果我们确定需要招募500名患者参加研究，以获得一些预设的效能来检测使用传统固定样本设计的临床治疗差异，其中信息量与样本量成正比，那么为了在成组序贯设计下有相同的效能来检验同样的治疗差异，我们需要招募的最大患者数是500 × IF，其中IF表示该成组序贯设计对应的膨胀因子。当然，每招募500×IF/K名患者并且完成终点指标的收集，将进行一次中期分析，最多进行K次，如果任何中期测试统计量超过了相应的边界，那么试验有可能因为优效而提前终止。

无效终止界值

在多次的期中分析时，如果药物没有相应的疗效，那么我们有可能提早的终止试验。这些因无效终止的界值的计算可参考优效终止的界值的方法。在备择假设下，超过无效终止界值的概率即为Ⅱ类错误（假阴性），而通过提前界定Ⅱ类错误可以通过β消耗函数来产生无效界值。为了保证在最后分析时无效界值和有效界值为一个，我们通常选择恰当的漂移参数η来界定。因此，在试验进行最终分析时，只存在拒绝零假设（优效）或接受零假设（无效）两种情况。其中η如下：

采用以下的迭代步骤来得到η，使得最后分析时无效界值和有效界值为一个：

1. 给定η一个初值。

2. 找出对成对的无效界值和有效界值（l₁，u₁）满足如下条件：\alpha(t_1)=P\left \{ Z(t_1)\ge u_1\mid H_0 \right \} , 和
   \beta(t_1)=P\left \{ Z(t_1)\le l_1\mid H_1 \right \} ,
   这里的u₁代表有效终止而l₁代表无效终止。

3. 对于k=2,…,K，可以递归解出两种不同的界值（l_k，u_k）：
   （绑定无效界值）binding futility boundary：\alpha(t_k) = \alpha(t_{k-1}) + \text{P}\{l_1 \leq Z(t_1) < u_1, \ldots, l_{k-1} < Z(t_{k-1}) < u_{k-1}, Z(t_k) \geq u_k | H_0\} \\ \beta(t_k) = \beta(t_{k-1}) + \text{P}\{l_1 < Z(t_1) < u_1, \ldots, l_{k-1} < Z(t_{k-1}) < u_{k-1}, Z(t_k) \leq l_k | H_1\}, \\ \text{with } \alpha(t_k) = \alpha \text{ and } \beta(t_k) = \beta. （非绑定无效界值）non-binding futility boundary：
   \alpha(t_k) = \alpha(t_{k-1}) + \text{P}\{ Z(t_1) < u_1, \ldots, Z(t_{k-1}) < u_{k-1}, Z(t_k) \geq u_k | H_0\} \\ \beta(t_k) = \beta(t_{k-1}) + \text{P}\{l_1 < Z(t_1) < u_1, \ldots, l_{k-1} < Z(t_{k-1}) < u_{k-1}, Z(t_k) \leq l_k | H_1\}, \\ \text{with } \alpha(t_k) = \alpha \text{ and } \beta(t_k) = \beta.

4. 重复步骤(1)-(3)直到解出η使得l_k=u_k。

结语

所以即使药物研发到上市过程中需要多个不同专业领域的通力合作耗费近十年的辛劳，但依旧摆脱不了药物本身的商品属性，所以抢占市场也变为及其重要的一环。因此在基于科学的准则下，如何更快的促使药物获批上市是一个重要的议题（假设药物真实有效），而我们今天所讨论的成组序贯设计（group-sequential design）就是其中的一种方法，诚然，加快药物上市或提高成功率的方法不止一种，等到有机会再和大家一起讨论学习。